2D Shock Wave/Laminar Boundary-Layer Interaction

Home > Sample Problems > Shock-Boundary Layer Interaction

2D Shock Wave/Laminar Boundary-Layer Interaction

Problem Description

The problem simulates the complex separated flow field generated by the impingement of an oblique shock on a laminar boundary layer developed along a flat plate. The flow conditions are freestream Mach number of 2.0, shock flow deflection angle 6º, and Reynolds number Re_L (based on the distance from the plate leading edge to the inviscid shock impingement location) equal to 3.0 ´ 10⁵.

Mesh

The size of the 2D computational domain is 286 ´ 131. The mesh grid is shown in Figure 1.

Figure 1. Computational Mesh

Simulation Parameters

The simulation parameters are summarized in Table 1.

Overall Flow Conditions
Mach No.	2.0
Reynolds No.	300000.0
Viscosity	laminar
Spatial Scheme
MUSCL	WENO 33	WENO 34
Time Scheme
BW2
2 subiteration per time step.
from a restart file		Final
Boundary Conditions
I=1: Inlet	Specified with the grid
I=286: Outlet	Outflow boundary condition: (Neumann for ρ, u, v, w, P)
J=1: Wall	Wall boundary condition (Specified wall temperature)
J=131	Freestream boundary condition: (Neumann for ρ, u, v, w, P)

Table 1. Simulation Parameters

Obtain the Files

Both mesh files and project input files can be accessed below. Remember to place the grid files in a subfolder with the set up file /shockbl.

Setup file (miguelplate.afl)

Grid file (myres.cgns).

Start the Simulation

Change the directory to the subfolder with the selected grid and spatial scheme. Start the simulation by

mpirun –np 1 mpiaeroflo.exe < shockbl.afl

Simulation Results

Figures 2, 3 and 4 show the pressure contours of flow field for MUSCL, WENO 33 and WENO 34 procedures, respectively.

Figure 2. Pressure contours in shock/boundary layer interaction region (MUSCL)

Figure 3. Pressure contours in shock/boundary layer interaction region (WENO 33)

Figure 4. Pressure contours in shock/boundary layer interaction region (WENO 34)

Comparison of Different Spatial Schemes

Figure 5 shows the surface pressure profiles for MUSCL and WENO procedures. The simulation results are also compared with Visbal and Gaitonde’s 3^rd-order Roe scheme simulation using the same size mesh grid and a fine (476 ´ 265) mesh grid, respectively. WENO 34 scheme provide better results compared with MUSCL results.

CFL Test

The CFL performances for different spatial schemes are also tested for this problem. The test results are summarized in Table 2.

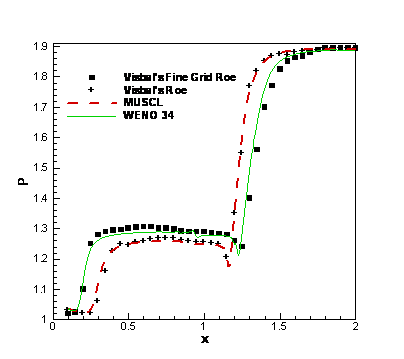
Figure 5. Surface pressure for Mach 2 shock/laminar boundary-layer interaction

	Spatial Scheme	Time Scheme	Turbulence Model	Grid Size Δs=min(Δx_i)	Test Value CFL= Δt/ Δs, CFL_a=(1+1/M)CFL
Converge (√) or Diverge(x)					√	√	x
Shockwave/Laminar Boundary Layer Interaction Ma=2.0	MUSCL	BW2	laminar	7.5E-5	1.0E-3 CFL=13.33 CFL_a=20	2.0E-2 CFL=266.67 CFL_a=400	3.0E-2 CFL=400 CFL_a=600 N=5841
	WENO 33	BW2	laminar		1.0E-3 CFL= CFL_a=	8.0E-2 CFL=1066.7 CFL_a=1600	9.0E-2 CFL=1200 CFL_a=1800 N=95
	WENO 34	BW2	laminar		1.0E-3 CFL= CFL_a=	1.0E-2 CFL=133.33 CFL_a=200	1.1E-2 CFL=146.67 CFL_a=220 N=2081

* The test is from the initial calculation.

** The CFL condition is computed by CFL= Δt/ Δs, which assume the reference flow velocity u=1.0.

*** Δs=min(Δx_i) is the minimum computational grid spacing

**** CFL_a=(u+a) Δt/ Δs=u(1+1/M)CFL is a measure of how far a sound wave can travel through the flow.

Table 2. CFL Number Test for Different Schemes

Reference:

Visbal, M. R. and Gaitonde, D. V., “Shock Capturing Using Compact-Differencing-Based Methods,” AIAA Paper 2005-1265.
M. Visbal – private communication.