Home   >  Sample Problems   >   Hypersonic Flow Past a Cylinder

 

Hypersonic Flow Past a Cylinder

 

Problem Description

 

 

Radius

1.5 in

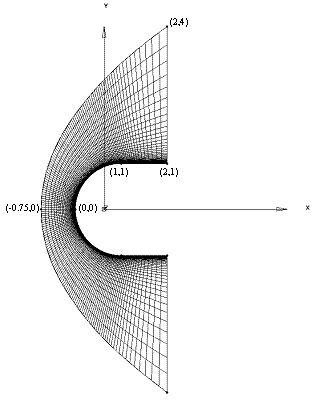
Figure 1. Hypersonic blunt body problem

M¥

16.34

Re

1.2 x 106 per foot

P¥

0.01203 psi

T¥

93.93 R

Twall

530 R

Surface Recell

3.7

Prandtl No

0.72

Sutherland parameter

2.1195

 

 

 

This test case represents a low-enthalpy flow for which the assumption of a perfect gas has been shown to be valid.  Experimental data for surface pressure and heat transfer rates exists. Numerical work comparing approximate Riemann solvers with flux-split methods has matched the experimental results.  Numerical results are often characterized by carbuncle phenomena, which can be suppressed through tuning of an entropy correction factor for some schemes.

 

Mesh

 

The computational mesh contains two 2D blocks. Both of the block sizes are 79 ´ 71.  The mesh geometry is shown in Figure 2.

 

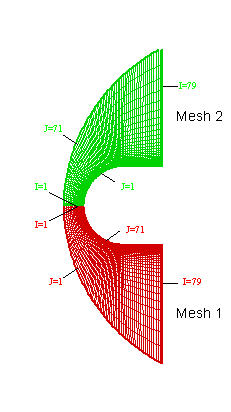
Figure 2. Computational Mesh

 

Simulation Parameters

 

Overall Flow Conditions

Mach No.

16.34

Viscosity

Laminar

Spatial Scheme

MUSCL

WENO 33

WENO 34

Time Scheme

BW2

Boundary Conditions

Block 1

I=1

Coupling to Block 2

I=79

Neumann for 老, u, v, w, p

J=1

老=1; u=1; v=0; w=0; p=0.002675

J=71

Solid wall;  老=66.25p

Block 2

I=1

Coupling to Block 1

I=79

Neumann for 老, u, v, w, p

J=1

Solid wall;  老=66.25p

J=71

老=1; u=1; v=0; w=0; p=0.002675

Initial Conditions

老=1; u=1; v=0; w=0; p=0.002675

Table 1. Simulation Parameters

Obtain the Files

 

Both mesh files and project input files can be accessed below. Remember to place the grid files in a subfolder with the set up file /Hyper.

Setup file (hyperbb.afl)

Grid files (2d_bg_dp_form.grd and 2d_tg_dp_form.grd).

 

Start the Simulation

 

Change the directory to the subfolder with the selected grid and spatial scheme. Start the simulation by

 

mpirun 每np 2 mpiaeroflo.exe < hyperbb.afl

 

The calculation starts from a small time step size 忖t = 1.0´10-6 for 10,000 steps. Then calculate the simulation with a larger time step size 忖t = 5.0´10-6 for 50,000 steps. Finally the simulation is calculated with a time step size 忖t = 1.0´10-5 for 1,000,000 steps.

 

 

Simulation Results

 

Figures 3, 4 and 5 are the nondimensionalized pressure contours for the MUSCL, WENO 33 and WENO 34 calculations, respectively.

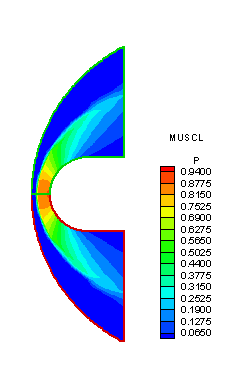
Figure 3. Nondimensionalized Pressure Contour (MUSCL)

 

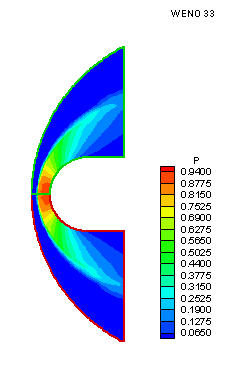
Figure 4. Nondimensionalized Pressure Contour (WENO 33)

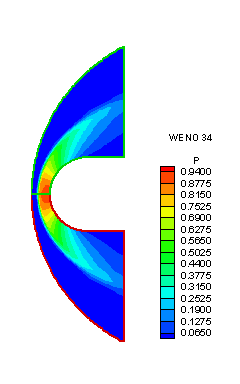
Figure 5. Nondimensionalized Pressure Contour (WENO 34)

 

 

Comparison of Different Spatial Schemes

 

Figure 6 shows the surface pressure distribution for different spatial schemes. The results are also compared with experimental results. Note that both of the WENO 33 and WENO 34 schemes blow out during the calculation.

 

Convergence Performance

 

Figure 7 compares the convergence performance of the three spatial schemes.

 

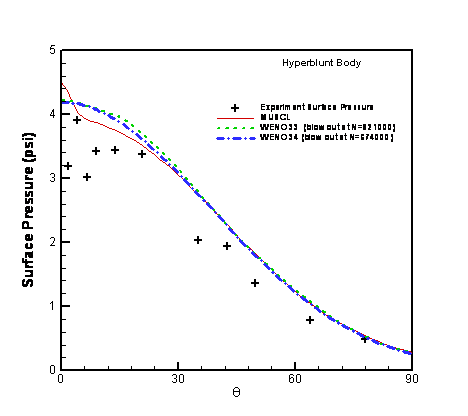
Figure 6. Surface Pressure with Comparisons of Experimental Data

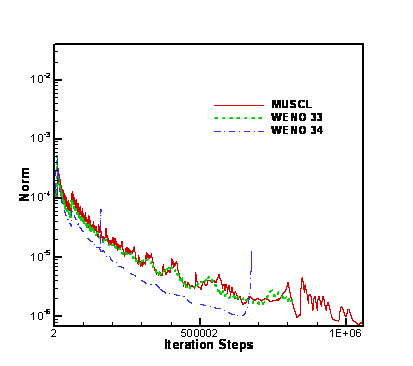
Figure 7. Convergence of Three Spatial Schemes

 

Reference:

 

1. R.K. Prabhu, J.R. Stewart, and R.R. Thareja. A Navier-Stokes Solver for High Speed Equilibrium Flows and Applications to Blunt Bodies.  AIAA Paper 89-0688, 1989

2. M.S. Holden, A.R. Wieting, J.R. Moselle, and C. Glass. Studies of Aerothermal Loads Generated in Regions of Shock/Shock Interaction in Hypersonic Flows. AIAA Paper 88-0477, 1988

3. D. Gaitonde, and J.S. Shang. The Performance of Flux-Split Algorithms in High-Speed Viscous Flows. AIAA Paper 92-0186, 1992

4. S. Sherer 每 private communication