Home   >  Sample Problems   >   Laminar Flow Over a Flat Plate

 

Laminar Flow Over a Flat Plate

 

Laminar flow over a flat plate is a problem that has been studied extensively, both analytically and experimentally. A solution to a simplified form of this problem can be obtained when several assumptions are made. These assumptions were first presented by Blasius in 1908. Comparisons of experiments with this solution have proved to be accurate.

 

Consider a flow at speed U past a thin plate of length L. The time a fluid particle spends near the body is approximately L/U, while the time required for viscous effects to spread across the streamlines is of order . If the diffusion time is much shorter than the residence time, the viscous region will be thin. This implies that the Reynolds number should be large enough. This condition is known to hold true in the region 1000< Re < 10⁶ outside of which the flow becomes turbulent.

 

The Blasius solution assumes that there is an inner boundary layer region below an outer region at which the flow remains the same as free stream conditions. A numerical simulation is set up to simulate the same conditions.

 

Computational Procedure

 

A Mach number of 0.1 and a Reynolds number of 1.0´10⁵ were chosen for the simulation.  The total computational domain extended two length units in the streamwise direction with a leading edge at x = 0. The extent of the domain in the normal direction is four length units. The computational grid employed 200 ´ 50 ´ 3 grid points in the i, j, and k directions, which also align with the x, y, and z axes respectively. The simulation type is simple CFD with compact scheme used for spatial differencing and the Beam-Warming scheme used for time differencing. The problem is solved as though two-dimensional in i and j directions. (Note that, although no spatial differencing is done in the k-direction, three grid points are still required in this direction as this is the minimum number of grid points allowed in any direction.)

 

The computational mesh is set up with graded elements close to the wall in the normal direction. In addition, the mesh is graded slightly in the streamwise direction, favoring more grid points close to the inlet. The computational mesh is shown in Figure P2.1(a). The initial conditions are as follows:

 

 

 

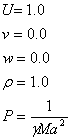
Obtain the Files

 

Both mesh files and project input files can be accessed below. Remember to place the grid files in a subfolder with the set up file /flateplate.

Setup file (flatplate.afl)

Grid file (flatplate.in).

 

Start the Simulation

 

Change the directory to the subfolder with the set up file. Start the simulation by

 

mpirun –np 1 mpiaeroflo.exe < flateplate.afl

 

 

Results

 

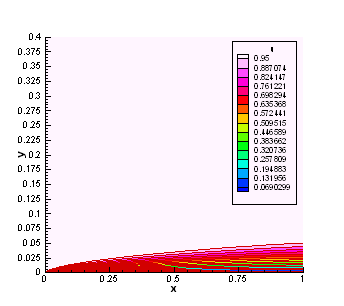
Figure 2.1(b) shows the u-velocity field following 68,000 iterations. Following an initial condition of u = 1.0 throughout the computational domain, a boundary layer has clearly formed on the plate starting from the leading edge.

    

(a)                                                        (b)

Figure P2.1 (a) Computation Mesh (b) u-velocity field showing the boundary layer developed on the flat plate

 

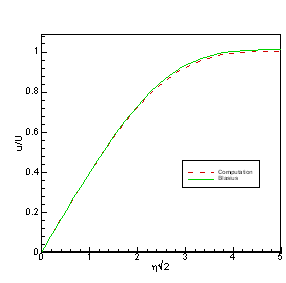
A comparison of the simulation at x = 1.7 with the Blasius profile is shown in Figure P2.2(a). Figure P2.2(b) shows the boundary layer thickness and displacement thicknesses compared with the Blasius solution. Note that the Blasius equation is an approximation of the complete Navier-Stokes equation with some of the terms ignored by analysis of the scales of the equations.

 

 

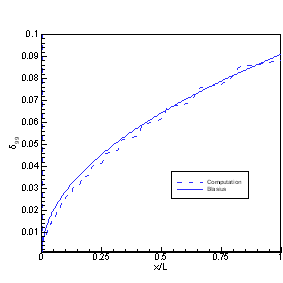
(a)                                                                                                                                        (b)

Figure P2.2 Comparison of simulation with the Blasius solution at x = 1.7 (a) u-velocity, (b) Boundary layer thickness

 

 

 

References:

White, F. M., “Viscous Fluid Flow”, 2^nd Ed., McGraw-Hill, 1991. pp 233-237.