Home   >  Sample Problems   >   Convergent-Divergent Duct

 

Convergent-Divergent Duct Problem

 

Problem Description

 

The duct test problem has been taken from Refs. [1-4]. Our predictions, in comparison with the experimental measurements, are shown in the next subsection. The agreement is excellent for the quantities compared. Details are presented below.

 

The physical domain has dimensions as shown in Fig. 1, where h_thr = 0.14435 ft is used as the dimensional length scale. This provides a Mach number of 0.46 at inlet and a Reynolds number of 687,810.4.

 

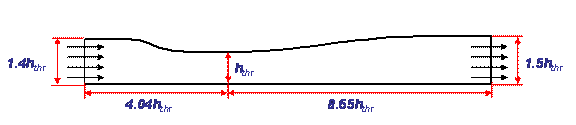
Figure 1 Physical domain for converging-diverging duct calculation

 

The inlet total pressure and outlet pressures are 19.58 psi and 16.05 psi, respectively, with non-dimensional values of 3.37564 and 3.19983, respectively. The total temperature is 500^oR. The density at the inlet is fixed at a non-dimensional value of 1.0. A non-dimensional velocity u = 1.0is applied at the inlet, while no-slip boundary conditions are imposed at the top and bottom walls. Dirichlet pressure boundary conditions are applied at the inlet and outlet, while zero Neumann boundary conditions are applied at the outlet for the other flow variables.

 

 

Mesh

 

An 81 ´ 51 grid was used to calculate flow through the duct with grid clustering in the vicinity of solid walls.  The mesh geometry is shown in Figure 2.

 

Figure 2. Computational Mesh

 

 

 

 

Simulation Parameters

 

 

Table 1. Simulation Parameters

 

Obtain the Files

 

Both mesh files and project input files can be accessed below. Remember to place the grid files in a subfolder with the set up file /cdvduct.

Setup file (cdvduct.afl)

Grid file (mesh-001.PLOT3D).

 

Start the Simulation

 

Change the directory to the subfolder with the set up file. Start the simulation by

 

mpirun –np 1 mpiaeroflo.exe < cdvduct.afl

 

Simulation Results

 

Figures 3, 4 and 5 are the Mach number contours for the MUSCL, WENO 33 and WENO 34 results.

 

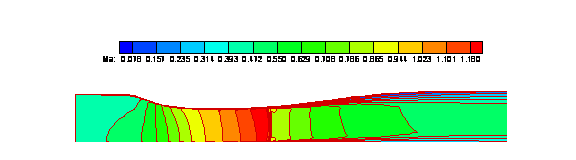
Figure 3. Mach Number Contour (MUSCL)

 

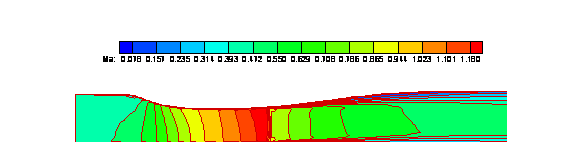
Figure 4. Mach Number Contour (WENO 33)

 

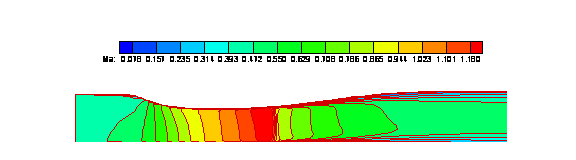
Figure 5. Mach Number Contour (WENO 34)

 

Comparison of Different Spatial Scheme

 

Figures 6 and 7 show the surface pressure distribution for different spatial schemes on the bottom wall and top walls, respectively. The results are also compared with experimental results. 

 

 

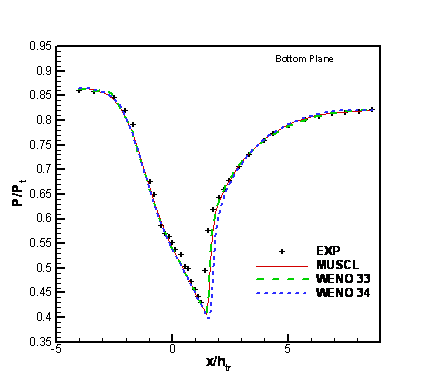
Figure 6. Pressure (Normalized by Total Pressure) Distribution along the Bottom Wall

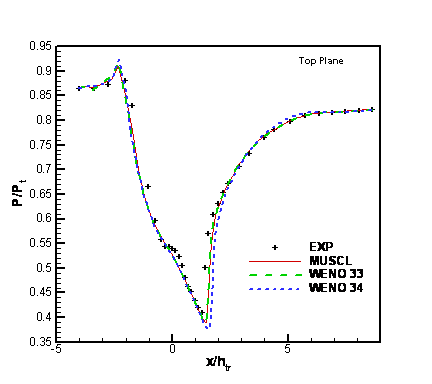
Figure 7. Pressure (Normalized by Total Pressure) Distribution along the Top Wall

 

 

 

Convergence Performance

 

Figure 8 compares the computation convergence speed for three spatial schemes.

 

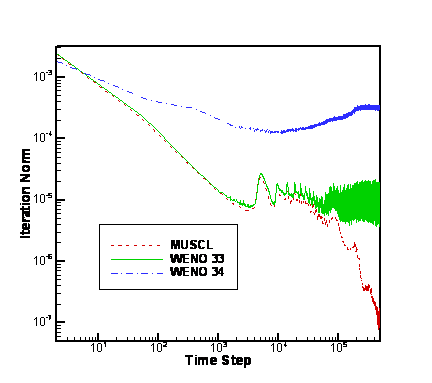
Figure 8. Convergence for Three Spatial Schemes

 

 

 

CFL Test

 

*  The CFL condition is computed by CFL= Δt/ Δs, which assume the reference flow velocity u=1.0.

** Δs=min(Δx_i) is the minimum computational grid spacing

*** CFL_a=(u+a) Δt/ Δs=u(1+1/M)CFL is a measure of how far a sound wave can travel through the flow.

 

Table 2. CFL Number Test for Different Schemes

 

 

 

 

Reference:

 

1. Bogar, T. J., Sajben, M., and Kroutil, J. C. (1983) "Characteristic Frequencies of Transonic Diffuser Flow Oscillations," AIAA Journal, Vol. 21, No. 9, pp. 1232-1240.
2. Bogar, T. J. (1986) "Structure of Self-Excited Oscillations in Transonic Diffuser Flows," AIAA Journal, Vol. 24, No. 1, pp. 54-61.
3. Chen, C. P., Sajben, M., and Kroutil, J. C. (1979) "Shock Wave Oscillations in a Transonic Diffuser Flow," AIAA Journal, Vol. 17, No. 10, pp. 1076-1083.
4. Sajben, M., Bogar, T. J., and Kroutil, J. C. (1984) "Forced Oscillation Experiments in Supercritical Diffuser Flows," AIAA Journal, Vol. 22, No. 4, pp. 465-474.
5. Salmon, J. T., Bogar, T. J., and Sajben, M. (1983) "Laser Doppler Velocimeter Measurements in Unsteady, Separated Transonic Diffuser Flows," Vol. 21, No. 12, pp. 1690-1697.